Digital signatures are nowadays ubiquitous and find application in secure com- munication protocols, code authentication, public key infrastructures and block- chain technologies. Control of funds deposited in any digital wallet is eventually based on the capability of its owner to prove ownership and sign transactions using an associated private key in a digital signature scheme.

One of the most widely adopted digital signature standards, based on elliptic curve cryptography (ECC), is ECDSA . Due to the high performance and small signature and key size, ECDSA has been adopted in many applications, from TLS to Bitcoin. A study conducted in early 2021 on the top market-cap 100 blockchains showed that 74 coins use ECDSA as digital signature scheme (over the secp256k1 curve ). The security of ECC is based on the difficulty of solving the discrete loga- rithm problem over the group of points of a suitable elliptic curve (ECDLP) and its related decisional variants ; however in practice, the theoretical security level can be degraded by the possibility to collect side channel information dur- ing the process of cryptographic operations as it has been first demonstrated on symmetric key algorithms and then extended to public key algorithms.
Indeed, physical leakage of secret data processed by embedded devices during sensitive operations, cache and memory accesses on mobiles, servers and desk- tops, combined with mathematical techniques allows to get around the hard ECDLP problem and to break security. In the case of ECDSA, thisoften translates to a compromise of the private key.The critical operation in ECC is the point-scalar multiplication, i.e. the op-eration that benefits from DLP-hardness. This can be viewed as the equivalentof modular exponentiation in RSA schemes. The scalar kwhich multiplies thecurve points can play different roles depending on the high level scheme which isinstantiating the point multiplication operation, but almost often its confiden-tiality is a primary concern. In Diffie-Hellman protocols, it represents a party’sprivate key (being ephemeral or static). In signature schemes such as ECDSAand Schnorr signatures , it is assumed to be a cryptographically strong ran-dom number (the nonce), and its confidentiality, integrity and non-repeatabilitymust always be assured.It is well known that if the value of even a single nonce used to generatean ECDSA signature is leaked, then anyone can retrieve the private key usedto generate the signatures. Therefore, all nonces must be kept secret. It is alsoknown that even if all nonces are kept secret, but a nonce value is reused formore than one signature, the private key can also be immediately retrieved.Such nonce collisions are very easy to detect, as the first half of each ECDSAsignature depends only on the nonce value (it can in fact be viewed as the publicephemeral key, or a public commitment to the nonce value used to generate thesecond half of the signature). Researches have also shown how biased generationof nonces can lead to unveiling of the private key, provided a sufficient numberof signatures is available (more details are given below).
1.1 Our Contributions
We advance the state of the art by proposing a novel attack that exploits high-degree relationships among the random values (nonces) used to generate sev-eral signatures, allowing to retrieve the signer’s private key. Our method is notexploiting any side channel information coming from the signature generationprocess, but is rather a cryptanalytic attack that can be run, under certain as-sumptions, on a relatively small set of signatures generated by a given privatekey.In our investigations, we make the assumption that nonces used to generateseveral ECDSA signatures are subject to an unknown polynomial relationshipmodulo n, where nis the order of the curve’s generator point; more precisely, wesuppose that they satisfy a recurrence polynomial equation of arbitrary degreeand unknown coefficients modulo n. In this case it is very easy to recover theprivate key using only few signatures, without the need of lattice reduction.The first step we need to perform is to find a way to get rid of the unknowncoefficients involved in the recurrence equation; to this purpose, we devise a re-cursive algorithm that is able to rewrite the unknown recurrence relation as apolynomial involving only differences of nonces. Then, we can use the relation-ships between the nonces and the private key given by the second half of eachsignature to rewrite the polynomial only in terms of the private key. Finally, we show that we can use known algorithms to find the roots of the polynomial; theprivate key will always be obtained as a root of the polynomial.The attack works on all prime curves currently standardized and in use forECDSA (including Bitcoin curve secp256k1) and up to our knowledge, it is thefirst to exploit relationships of degrees higher than linear.Cases where nonces are generated with Linear Congruential Generators (LCG),quadratic or cubic generators with unknown coefficients modulo n, are specialcases of this general category of relationships. After showing how to attack noncesgenerated with an arbitrary recurrence relation, we then prove that even sets offully random nonces allow the attacker to retrieve the private key when the setis completed by one additional nonce that follows the (unknown) recurrence re-lation given by the random nonces taken in a given order (we refer to this asthe rogue nonce example). When a sufficient number of signatures are gener-ated with a given private key, there will always be a reordering of the signaturesthat make the recurrence attack work, leading to compromise of the private key.However, we are not able to find this ordering faster than brute-force.
1.2 Related Work
The generation of an ECDSA signature is arguably a fragile process, requiring thecreation and use of cryptographically strong random values; it is understandablethat its security has been widely scrutinized and that attacks exploiting badimplementations have been extensively published.In the ANSI X9.62 document, the group where the DLP-hard operationtakes place is the group on the curve defined by the generator point G, whichhas order n. Therefore it seems then natural to assign the requirement thatk∈[1, n−1], where nis the order of the generator point of the elliptic curve. Thisconstraint is coherent with the fact that private keys in elliptic curve key pairsmust be chosen uniformly randomly over the same interval (in the document theper-message secret kis indeed referred-to as an ephemeral key).When kis chosen, a scalar-point multiplication is performed to obtain thecorresponding public key R= [k]Gand the signature rpart is determined asthe x-coordinate of R. To mitigate the usefulness of partial information obtainedfrom the process of computing R= [k]G, the value of kcan be blinded bypreliminary addition of a random multiple of n, where the multiplication factormust have at least log2n2bits . The partial information could be an MSBprefix of the scalar k, that can be used to retrieve the private key by solvinginstances of the hidden number problem [12] by means of lattice reduction [27].Even if the ECDSA signature generation is performed securely, if the noncevalues kare not properly generated in a random way, attacks become possible.An example would be if the kvalues are biased, that is if their distribution overthe interval [1, n −1] is not uniform. for example if they contain known prefixes,suffixes or common bit sequences [18], or if they are generated using non crypto-graphic PRNGs [13],[21],[8]. This latter case is particularly interesting; if noncesare generated using Linear Congruential generators (LCGs), the signatures can be likely used to mount an attack by means of Lattice Reduction algorithms[19], and the signer’s key can be obtained.The biases used in [19], [13] and exploited so far in the literature can be seenas simple relations between the nonce bits, or linear relations between the fullnonce values. Up to our knowledge, there are no published studies on cases wherethe nonce values are related in a more complicated way, for instance by means ofquadratic, cubic or higher-degree algebraic relationships. This will be our goal,and is motivated by the fact that examples of non-cryptographic PRNGs includequadratic and cubic congruential generators [32].The rest of this paper is organized as follows: Section 2covers preliminariesuseful to understand the rest of the paper; Section 3presents the attack; Section4discusses an implementation and give some results, Section 5concludes thepaper.
2 Preliminaries
In this section we give the required preliminaries that are going to be used inthe rest of this work. In the following, we use “iff” as “if and only if”, DLP as“discrete logarithm problem” and ECDLP as “elliptic curve discrete logarithmproblem”. By algorithm or procedure we mean a uniform family of circuits ofdepth and width polynomial in the index of the family. Namely: F={Fn}n∈Nis an algorithm iff there exists an integer ¯n, polynomials τ, w, d and a Turingmachine MFwhich, given nas input, outputs a description of Fnin time atmost τ(n) for any n > ¯n, where Fnis a Boolean circuit of width at most w(n)and depth at most d(n). If an algorithm Ais deterministic, we denote its outputyon input xas y:= A(x), while if it is randomized we use y←A(x). We willalso use xD←−− Xto denote that an element xis sampled from a distribution Dover a set X(or simply x← D when the image set is implied); or we will writex$←− Xif xis sampled uniformly at random from a set X. We will call negligible(and denote by negl(n)) a function that grows more slowly than any inversepolynomial in n, and overwhelming a function which is 1 minus a negligiblefunction. Finally, a∥bdenotes concatenation of strings.
2.1 Cryptographic Primitives
A Weierstrass elliptic curve Edefined over a finite field Fqis a set of points
P= (x, y) where xand ybelongs to Fqand satisfy a certain equation curve E,
together with the point at infinity denoted by O:
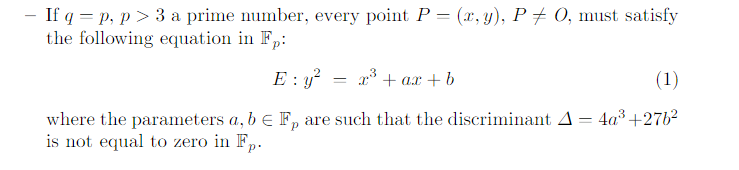

This operation is directly linked to the ECDLP and provides security in
all cryptographic schemes based on ECC. Its execution time and its sensitivity
regarding physical attacks are major concerns when ECC is implemented in
HW and/or SW. Several regular algorithms are available to execute securely the
scalar point multiplication, for details we refer to [15] and [20]
2.2 ECDSA
Let us represent the ECDSA domain parameters as DECDSA = (q, a, b, G, n, h),the key pair be (d, Q) with Q= [d]Gand the required hash function being h(.).The process of generating an ECDSA signature is given in Algorithm 1.To produce digital signatures, a random or pseudo-random per-signaturesecret kmust be generated, consumed and discarded. It can also be determinis-tically generated [30] , but in any case its secrecy must be guaranteed becauseits leakage enables to retrieve the signer’s private key

One quickly realizes that the sensitivity of kis equivalent to the sensitiv-ity of the signer’s private key, and therefore special care must be taken versusimplementation attacks, including physical attacks, when kis manipulated.During signature generation, kis used three times. The first time is to com-pute rvia scalar point multiplication, the second time to obtain its modularinverse k−1mod nand the last time in its inverse form during scomputation.None of these operations should leak any information on the bits of k.
3 The New Attack
3.1 A Generic Observation
Suppose that Nsignatures are generated using the ECDSA algorithm usingthe same private key d; let us denote the parameters of the i-th signature as(ki, hi, ri, si) where kdenotes the nonce, hthe message hash, rthe first half ofthe signature and sthe second half of the signature. All equations in the rest ofthis paper are intended modulo n, where nis the order of the curve’s generatorpoint G. For each generated signature we can write:
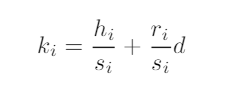
In other words, the second half of every signature gives us a linear relationbetween the used nonce and the private key, as the message hash value and thetwo halves of each signature are public and known. We believe this is, by itself,an interesting observation. As the first half of every signature is the x coordinateof the point Ri= [ki]G, it is straightforward to use the curve equation to obtainthe point Ri(up to a sign of its y coordinate, here we can make the assumptionof taking the smallest value of y). Obtaining kifrom Riwould mean solving thediscrete logarithm problem over the curve; but indeed using the second halvesof the signatures, we can write a relationship between the nonce values. Takingthe example case of two signatures, it is easy to verify that we can re-write (6)as:
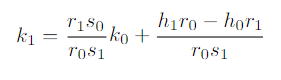
and, multiplying times the generator point G, we obtain (regrouping knownvalues in a, b):
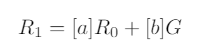
which is a non-trivial relationship that one is not supposed to write knowingonly the nonce commitments (i.e. the points Ri).This shows that given the set of Npoints Ri, we are not confronted with Ninstances of the discrete logarithm problem, but with only one instance, as weknow how all these nonce values are related, through the private key dby meansof the values of si. This is, after all, the reason behind the well known fact thatknowledge of one ECDSA nonce value is equivalent to knowledge of the privatekey, and also to knowledge of all nonce values ever used to generate signatureswith that particular private key.When the nonces used for Nsignatures obey a multivariate polynomial equa-tion, we can rewrite the equation as a univariate polynomial involving only theprivate key and public values by substituting the relations above. For example,if we know coefficients aiand exponents eisuch that
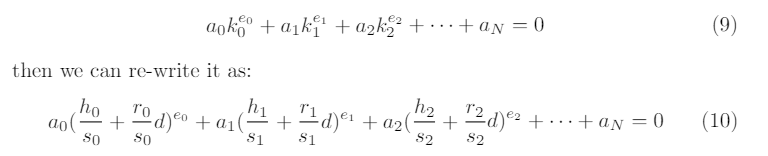
Now, this is a polynomial of degree maxi(ei) in the unknown d. Algorithmsexist to quickly expand and find roots of such polynomials over finite fields(for instance, Berlekamp’s algorithm[11]) and are often implemented in freelyavailable computer algebra packages, such as SageMath [5] for instance; theprivate key dwill always appear among the roots of the polynomial. Note thatmore complex relations where the nonces are multiplied together will also work,as for example
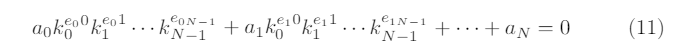
can also be re-written as above and will also lead to a univariate polynomial ind(with potentially higher degree). The natural question that arises is how tofind such relation between the nonces; if they are chosen in a properly randomway, this is generally not possible. However, in some cases it may be possible towrite such relation, as we will see in the next sections.
3.2 Nonces generated with an (unknown) recurrence equation
Let us consider the case where the signer generates NECDSA signatures choos-
ing the first nonce k0at random and all the following N−1 nonces using a
(N−3)-degree recurrence relation with N−2 unknown coefficients. We can
think about this as the most general case of a polynomial random number gen-
erator with secret coefficients ai, seeded by the initial state k0
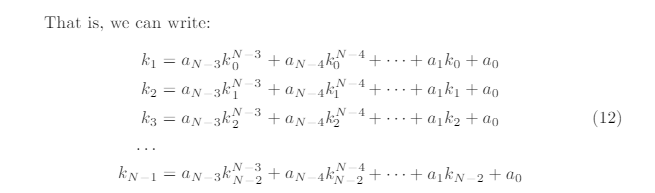
What we want is to write a polynomial involving only the nonces, and toget rid of the unknown recurrence relation coefficients ai, so that we can thenrewrite the equation with only the private key. Let us tackle the general case byanalyzing the simplest cases first, and then proceed with a recursive algorithm.When N= 4, we are essentially looking at the simple case of an LCG withunknown multiplier a1, increment a0and initial state k0, that is:


Indeed, we can show that the polynomials involving the nonces generated by(12) can be obtained using a recursive algorithm that constructs polynomialsusing the nonces differences ki,j ; then, substituting the values with (19) leads toa polynomial in dthat can be solved to obtain the private key.The recursive algorithm has been constructed by inspection and generaliza-tion of the hand-constructed polynomials shown above for N= 4,5,6 and hasbeen tested to work for Nup to 16. The degree in dof the polynomial for Nsignatures is equal to 1 + PN−3i=1 i. The polynomial in terms of the ki,j for Nsig-natures can be obtained by calling the recursive function dpoly(N−4, N −4,0)where the function dpoly is described in Algorithm 2.

3.3 Adding a carefully crafted signature to an existing set
Let us now consider the case where the signer has correctly generated N−1nonces in a random way, and has so produced a set of N−1 signatures. Theconsiderations of the previous section are not valid for this set, but if we take alook at (12) we can see that they describe a rather generic recurrence equation.The fact that the coefficients are unknown and we do not make assumptionson them, lead to the following consideration: let us take all equations from (12)but the last one. We have a set of N−2 equations binding the N−1 noncesvia the N−2 coefficients ai. Therefore, for a given set of such N−1 randomlygenerated nonces, one can always obtain one solution, i.e. one set of coefficientsaithat binds them with a recurrence relation of degree N−3.In other words, even for a set of random nonces, there always exists animplicit unknown recurrence equation of the form (12) that binds them. Now,if we complete the set of signature with an additional one, where the nonce ischosen to satisfy the recurrence equation, we are back in the case analyzed inthe previous section, and we can simply obtain the signer’s private key using thetechnique explained above.We can refer to this additional nonce as the rogue nonce. Note that by chang-ing the order of the first N−1 signatures, one obtains different values for theimplicit recurrence relation coefficients, and therefore a different value of therogue nonce. When the value of Nhas the order of magnitude of the numberof bits of the curve, it is easy to see that given a set of properly generated Nsignatures, it is always possible to re-order the first N−1 ones to make the lastsignature fit the underlying implicit recurrence relation.This follows from thefact that the number of permutations grows with the factorial or approximatelyNN, which is greater than 2N. Therefore given a big enough set of signatures,there will always be a given re-ordering that allows the retrieval of the privatekey by means of the attack proposed above. All of this is only of theoreticalinterest, as we are not able here to devise a way of finding this re-ordering easierthan with brute-force.

4 Implementation And Benchmarks
The techniques presented in this paper have been implemented in Python lan-guage, using the SageMath Python extensions. SageMath [5] is a powerful toolthat is able to execute Python programs in a native way and gives to the pro-grammer a powerful set of algebraic manipulation routines; these can be used toconstruct polynomials, manipulate them and find roots.The code for the related nonces and the rogue nonce cases can be foundin this GitHub repository [1], under the original_attack folder. To executethem, it is necessary to invoke Sage and to install the Python ecdsa, hashlib andrandom libs. Retrieval of the private key from a set of signatures takes roughly70 ms on average a common laptop for the sec256k1 curve, about 340 ms onaverage for the NIST secp384r1 curve, and about 490 ms on average for thesecp521r1 curve; these numbers do not vary significantly for linear, quadratic orcubic recurrence equations. When N= 16, the algorithm takes about 6.5 s toretrieve the private key.We used this code as a basis to conduct a scan of the Bitcoin and Ethereumblockchains, to spot possible usages of such weak PRNGs for ECDSA signaturegeneration. We were not able to obtain results, but we re-discovered cases ofusage of repeated nonces. Indeed, a repeated nonce is a trivial case of the re-currence relation studied in this paper, where the only non-zero coefficient is a0,which is equal to the repeated nonce; details on our experiments can be foundhere.Complete source code can be found in the GitHub repositories [1], [2] forBitcoin ECDSA signatures dumping code, [3] for Ethereum ECDSA signaturesdumping code. We also tried the attack without results on dumps of TLS con-nection establishments, see the GitHub repository [4] for more details.
5 Conclusions and Future Directions
n this paper we presented an attack that exploits the existence of generic nonlin-ear (high-degree) algebraic relations between ECDSA nonces in order to retrieve the signer’s private key. We studied the case of a generic recurrence relation ofdegree N−3 with unknown coefficients, showing that Nsuch signatures allowthe attacker to obtain the private key in negligible time. We have also shownthat given a sufficiently large collection of signatures generated with uniformlyrandom nonces, there is an ordering of the signatures which would allow easyretrieval of the private key by means of the attack proposed here.We see several lines of extension of our work. First, we would like to remarkthat the considerations presented here certainly apply also to other signatureschemes that require the generation of a random nonce (or ephemeral secret), forinstance Schnorr signatures. Deterministic variants (e.g. deterministic ECDSAand EdDSA [25]) make use of cryptographic hash functions to generate thenonces and are thus inherently resistant to the attacks described here.It would be interesting to devise techniques that would allow retrieval ofthe private key in the case where the modulo used by the recurrence relationis different from the order of the curve, as this seems an interesting case forknown LCG, QCG and CCG such as the ones referenced in [32]. Even if itwould probably be necessary to make further assumptions, for instance that themoduli should be co-prime, we consider this as the most interesting evolution ofthe work presented here.It would be nice to devise a way to find signature reordering faster than withbrute-force, for the case where a rogue nonce is considered. For experimentaltrials, we were rather limited by the latency of the process, especially becausethe proposed attack works only if the generated signatures are taken in thesame order with which they have been chronologically generated (or the exactopposite one); it would be interesting to try to extend the search scope, possiblytargeting other blockchains and/or protocols. It could also be possible to avoidthe use of SageMath, and to code the attack natively with low-level languages,allowing compilation and optimization; this would probably boost the speed fora widespread search for weaknesses.A negative check for the success of the attack could be integrated for instancein existing libraries [19]; the goal would be to exclude such conditions that wouldallow compromising the signer’s private key
5.1 Acknowledgements
The author would like to thank Nils Amiet for his work on the implementationof the attack and the tests against the blockchain signatures (see Section 4) andTommaso Gagliardoni and Karine Villegas for the fruitful discussions and forrevising preliminary versions of this paper.


